PIC'S , ASM Y C, PRACTICAS DE ELECTRONICA

Un vector puede ser representado graficamente por una flecha para indicar la dirección. La punta de la flecha es la "cabeza" del vector, y el otro extremo su "cola". Las operaciones básicas pueden llevarse a cabo graficamente representando a los vectores así, independientemente del sistema coordenado.

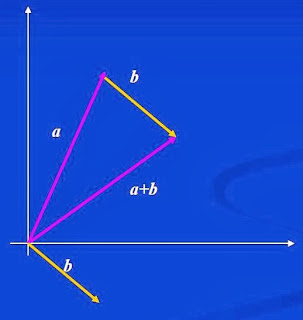
• SUMA DE VECTORES

La cabeza de un vector se conecta con la cola de otro, sin cambiar su orientación relativa.

 Suma del vector A con el  B, representacion gráfica.

También se puede representar graficamente la suma de la siguiente forma.

Dos vectores A y B pueden sumarse para dar otro vector C; esto es:

 La suma de dos vectores se efectúa componente por componente, si se tienen dos vectores A y B.

Entonces la suma nos queda:

  
Ejemplo:

Si se tienen los siguientes vectores:

 Realizar la suma C=A+B:



 Graficamente se ven los vectores de la siguiente manera:


  

•  RESTA DE VECTORES      

Se hace igual que la suma, pero invirtiendo la dirección del vector que debe restarse.


Alternativamente, pueden conectar los dos vectores cola con cola, y el vector resultante sera el que una las dos cabezas.


Dos vectores A y B pueden restarse para dar otro vector C; esto es:


La resta de dos vectores se efectúa componente por componente, si se tienen dos vectores A y B.  
 Entonces la resta nos queda:


Ejemplo:

Si se tienen los siguientes vectores:


Realizar la resta C=A-B:




Graficamente se ven los vectores de la siguiente manera:


Las graficas de los ejemplos se realizaron con Maple 13.

•  MULTIPLICACIÓN POR UN ESCALAR

En este caso cambia la magnitud del vector y su dirección en 180º si el escalar es negativo. La multiplicación por un escalar se ilustra en la siguiente figura.


Cualesquiera vectores dados A, B y C obedecen estas tres leyes algebraicas básicas:


Nota: l y k son escalares.

Referencias:

• Elementos de electromagnetismo, Matthew N. O. Sadiku
• Teoría electromagnética, Roberto S. Murphy Arteaga